R code
# packages used
library("data.table")
library("ggplot2")
library("ggradar") # ggplot2 compatible radar chartsSpiders, facets, and dots, oh my!
R
ggplot2
data storytelling
magick
chart design
A case study comparing the effectiveness of a radar chart to a faceted dot chart.
At a recent virtual workshop, a participant asked my opinion of radar charts (also called spider charts). I replied that I think there are nearly always more effective alternatives.
Other authors agree, e.g., Graham Odds (2011) and Stephen Few (2005), concluding that bar charts or line charts communicate information more effectively than radar charts in nearly every case. I concur, but I thought it would be interesting to compare a radar chart to an alternative using somewhat more complex data than those in typical examples.
I selected data from a 1951 chart by graphic designer Will Burtin (1908–1972) displaying the effectiveness of three antibiotics in inhibiting the growth of 16 bacteria. My inspiration is Medical Illuminations (2014) in which Howard Wainer discusses in detail twenty different charts of these data. In this post, I compare two new displays of these data—a radar chart and a faceted dot chart.
For reproducibility, the R code for the post is listed under the “R code” pointers.
For consistent radar charts, I wrap ggradar() in a custom function. I selected the ggradar package because it supports editing using conventional ggplot2 functions.
R code
# custom function for consistent radar charts
make_radar_chart <- function(dframe, subtitle) {
# assign constants
tick <- 0.3
grid_lines <- c(-3, -1, 3)
medium_gray <- "gray70"
# delete all but the required columns
dframe <- dframe[, .(Bacteria, Penicillin, Streptomycin, Neomycin)]
# create the radar chart using a subset of the data frame
ggradar(plot.data = dframe,
# three grid lines allowed
values.radar = grid_lines,
grid.min = grid_lines[1],
grid.mid = grid_lines[2],
grid.max = grid_lines[3],
# manual adjustments for clear viewing
gridline.label.offset = 1.5,
plot.extent.x.sf = 1.5,
plot.extent.y.sf = 1.25,
centre.y = -4,
# aesthetics
background.circle.colour = "transparent",
grid.label.size = 5,
group.line.width = 0.5,
group.point.size = 3) +
# ggplot2 edits, including tick marks along the P-axis
labs(subtitle = subtitle) +
theme(plot.subtitle = element_text(size = 18,
face = "bold",
hjust = 0,
vjust = -4,
color = medium_gray),
legend.justification = c(0, 1),
legend.background = element_blank(),
legend.key.height = unit(6, "mm"),
legend.position = c(-0.04, 0.93), # c(-0.04, 1.05),
legend.text = element_text(size = 12, face = "italic"),
legend.title = element_blank()) +
geom_segment(x = -tick, y = 2, xend = tick, yend = 2, color = medium_gray) +
geom_segment(x = -tick, y = 4, xend = tick, yend = 4, color = medium_gray) +
geom_segment(x = -tick, y = 5, xend = tick, yend = 5, color = medium_gray) +
geom_segment(x = -tick, y = 6, xend = tick, yend = 6, color = medium_gray)
}Data
I transcribed the data from Wainer (Table 2.1, p. 24) but updated the taxonomy of two bacteria that have been renamed since Burtin’s work.
In 1974, Diplococcus pneumoniae was renamed Streptococcus pneumoniae. In 1984, Streptococcus faecalis was renamed Enterococcus faecalis.
One of Wainer’s goals was to illustrate how some chart designs, had they been investigated sooner, could have revealed an odd pattern in Burtin’s data that might have led to an earlier reclassification of bacterium genus. My goal is different. I want to illustrate the relative effectiveness of two specific charts by considering the ease and accuracy of answering key domain-specific questions about the data.
The data with current taxonomy are saved in the blog data directory as a CSV file.
R code
# read the updated Burtin data set
DT <- fread("data/antibiotic-bacteria-mic.csv")
# examine the data
DT[] Bacteria Gram_stain Penicillin Streptomycin Neomycin
<char> <char> <num> <num> <num>
1: Aerobacter aerogenes negative 8.7e+02 1.00 1.600
2: Bacillus anthracis positive 1.0e-03 0.01 0.007
3: Brucella abortus negative 1.0e+00 2.00 0.020
4: Streptococcus pneumoniae positive 5.0e-04 11.00 10.000
5: Escherichia coli negative 1.0e+02 0.40 0.100
---
12: Staphylococcus albus positive 7.0e-03 0.10 0.001
13: Staphylococcus aureus positive 3.0e-02 0.03 0.001
14: Enterococcus faecalis positive 1.0e+00 1.00 0.100
15: Streptococcus hemolyticus positive 1.0e-03 14.00 10.000
16: Streptococcus viridans positive 5.0e-03 10.00 40.000The data set comprises three categorical variables and one quantitative variable as listed in Table 1. The quantitative variable is the minimum inhibitory concentration (MIC)—the least concentration of antibiotic that prevents growth of a bacterium in vitro, where concentration is the ratio of the drug to its liquid media in milligrams/deciliter (mg/dl).
| variable | structure |
|---|---|
| bacteria | categorical, nominal, 16 levels |
| antibiotic | categorical, nominal, 3 levels |
| min. inhibitory concentration (MIC) | quantitative (mg/dl) |
| Gram stain | categorical, 2 levels, dependent on bacteria |
The Gram stain variable indicates a bacterium’s response to a cell-staining method, named after bacteriologist Hans Christian Gram (1853–1938). After staining and counter-staining, those that remain purple are called Gram-positive; those that turn pink are called Gram-negative.
Shaping the data
I’m not using Gram staining as a graph element, so I append the Gram-positive information to the name of the bacterium and drop the Gram-staining variable.
R code
# append Gram-positive to bacteria names
DT[Gram_stain == "positive", Bacteria := paste(Bacteria, "(+)")]
DT[, Gram_stain := NULL]
# display the result
DT[] Bacteria Penicillin Streptomycin Neomycin
<char> <num> <num> <num>
1: Aerobacter aerogenes 8.7e+02 1.00 1.600
2: Bacillus anthracis (+) 1.0e-03 0.01 0.007
3: Brucella abortus 1.0e+00 2.00 0.020
4: Streptococcus pneumoniae (+) 5.0e-04 11.00 10.000
5: Escherichia coli 1.0e+02 0.40 0.100
---
12: Staphylococcus albus (+) 7.0e-03 0.10 0.001
13: Staphylococcus aureus (+) 3.0e-02 0.03 0.001
14: Enterococcus faecalis (+) 1.0e+00 1.00 0.100
15: Streptococcus hemolyticus (+) 1.0e-03 14.00 10.000
16: Streptococcus viridans (+) 5.0e-03 10.00 40.000I order the bacteria by the median of their three MIC values (per Wainer) and add a lowercase letter (a.–p.) to the bacteria names to provide a simple verification that the charts reflect the desired order.
Because MIC values span several orders of magnitude, I also apply a log10 transformation to the numerical columns.
R code
# order bacteria by row-wise median MIC
DT[, median_MIC := apply(.SD, 1, median), .SDcols = c("Penicillin", "Streptomycin", "Neomycin")]
setorder(DT, median_MIC)
# lowercase letters to verify bacteria order in the charts
DT[, order_ID := letters[1:nrow(DT)]]
DT[, Bacteria := paste0(order_ID, ". ", Bacteria)]
DT[, order_ID := NULL]
# transform MIC by log10
numeric_cols <- which(sapply(DT, is.numeric))
DT[ , (numeric_cols) := lapply(.SD, log10), .SDcols = numeric_cols]
# display the result
DT[] Bacteria Penicillin Streptomycin Neomycin
<char> <num> <num> <num>
1: a. Bacillus anthracis (+) -3.000 -2.000 -2.155
2: b. Staphylococcus albus (+) -2.155 -1.000 -3.000
3: c. Staphylococcus aureus (+) -1.523 -1.523 -3.000
4: d. Proteus vulgaris 0.477 -1.000 -1.000
5: e. Escherichia coli 2.000 -0.398 -1.000
---
12: l. Pseudomonas aeruginosa 2.929 0.301 -0.398
13: m. Mycobacterium tuberculosis 2.903 0.699 0.301
14: n. Streptococcus pneumoniae (+) -3.301 1.041 1.000
15: o. Streptococcus hemolyticus (+) -3.000 1.146 1.000
16: p. Streptococcus viridans (+) -2.301 1.000 1.602
median_MIC
<num>
1: -2.155
2: -2.155
3: -1.523
4: -1.000
5: -0.398
---
12: 0.301
13: 0.699
14: 1.000
15: 1.000
16: 1.000Clinically plausible dosages are those less than 0.1 mg/dl or log10MIC ≤ –1. Thus concentrations greater than –1 indicate a bacterium that for clinical purposes can be considered resistant to the antibiotic.
Wainer illustrates (in Figure 3.3 by Brian Schmotzer, p. 54) that this resistance measure, summarized in Table 2, is a useful criterion by which the data in a chart can be organized to answer key questions.
| Label | Bacterium is resistant to |
|---|---|
| None | None of the three antibiotics |
| P | Penicillin only |
| PS | Penicillin and Streptomycin only |
| SN | Streptomycin and Nemomycin only |
| PSN | All three antibiotics |
I add these resistance labels to the data frame, creating a new categorical variable (resistance) that is dependent on the bacteria.
R code
# classify bacteria by resistance
DT[, resistance := fcase(
Penicillin > -1 & Streptomycin > -1 & Neomycin > -1, "PSN",
Penicillin > -1 & Streptomycin > -1 & Neomycin <= -1, "PS",
Penicillin <= -1 & Streptomycin > -1 & Neomycin > -1, "SN",
Penicillin > -1 & Streptomycin <= -1 & Neomycin <= -1, "P",
Penicillin <= -1 & Streptomycin <= -1 & Neomycin <= -1, "None"
)]
# display the result
DT[] Bacteria Penicillin Streptomycin Neomycin
<char> <num> <num> <num>
1: a. Bacillus anthracis (+) -3.000 -2.000 -2.155
2: b. Staphylococcus albus (+) -2.155 -1.000 -3.000
3: c. Staphylococcus aureus (+) -1.523 -1.523 -3.000
4: d. Proteus vulgaris 0.477 -1.000 -1.000
5: e. Escherichia coli 2.000 -0.398 -1.000
---
12: l. Pseudomonas aeruginosa 2.929 0.301 -0.398
13: m. Mycobacterium tuberculosis 2.903 0.699 0.301
14: n. Streptococcus pneumoniae (+) -3.301 1.041 1.000
15: o. Streptococcus hemolyticus (+) -3.000 1.146 1.000
16: p. Streptococcus viridans (+) -2.301 1.000 1.602
median_MIC resistance
<num> <char>
1: -2.155 None
2: -2.155 None
3: -1.523 None
4: -1.000 P
5: -0.398 PS
---
12: 0.301 PSN
13: 0.699 PSN
14: 1.000 SN
15: 1.000 SN
16: 1.000 SNRadar charts
This data frame is correctly shaped for ggradar() in row-record form, in which every record about a bacterium is in a single row.
Explaining a radar chart
I subset one bacterium (one row and four columns) from the data frame to illustrate radar-chart terminology in Figure 1.
R code
# select one row only from the data set
data_group <- DT[Bacteria %ilike% "abortus", .(Bacteria, Penicillin, Streptomycin, Neomycin)]
# display the result
data_group[]
# create the sample radar chart
p <- make_radar_chart(data_group, subtitle = "Radar chart components")
# annotate the features of the chart
p +
geom_text(x = 2.5, y = 2.5, label = "dosage max grid line",
hjust = 0, vjust = 1, size = 4, color = "gray45") +
geom_text(x = -0.1, y = 5.7, label = "P-axis",
hjust = 1.1, size = 4, color = "gray45") +
geom_text(x = -4, y = -3.1, label = "N-axis",
hjust = 0.3, size = 4, color = "gray45") +
geom_text(x = 4.1, y = -3.1, label = "S-axis",
hjust = 0.7, size = 4, color = "gray45") +
geom_text(x = 5.5, y = 5.5, label = "scale max grid line",
hjust = 0, vjust = 1, size = 4, color = "gray45") +
geom_text(x = 5, y = -1.6, label = expression("log"[10]~"MIC"),
hjust = 0.2, vjust = 0.8, size = 4, color = "gray45") Bacteria Penicillin Streptomycin Neomycin
<char> <num> <num> <num>
1: h. Brucella abortus 0 0.301 -1.7
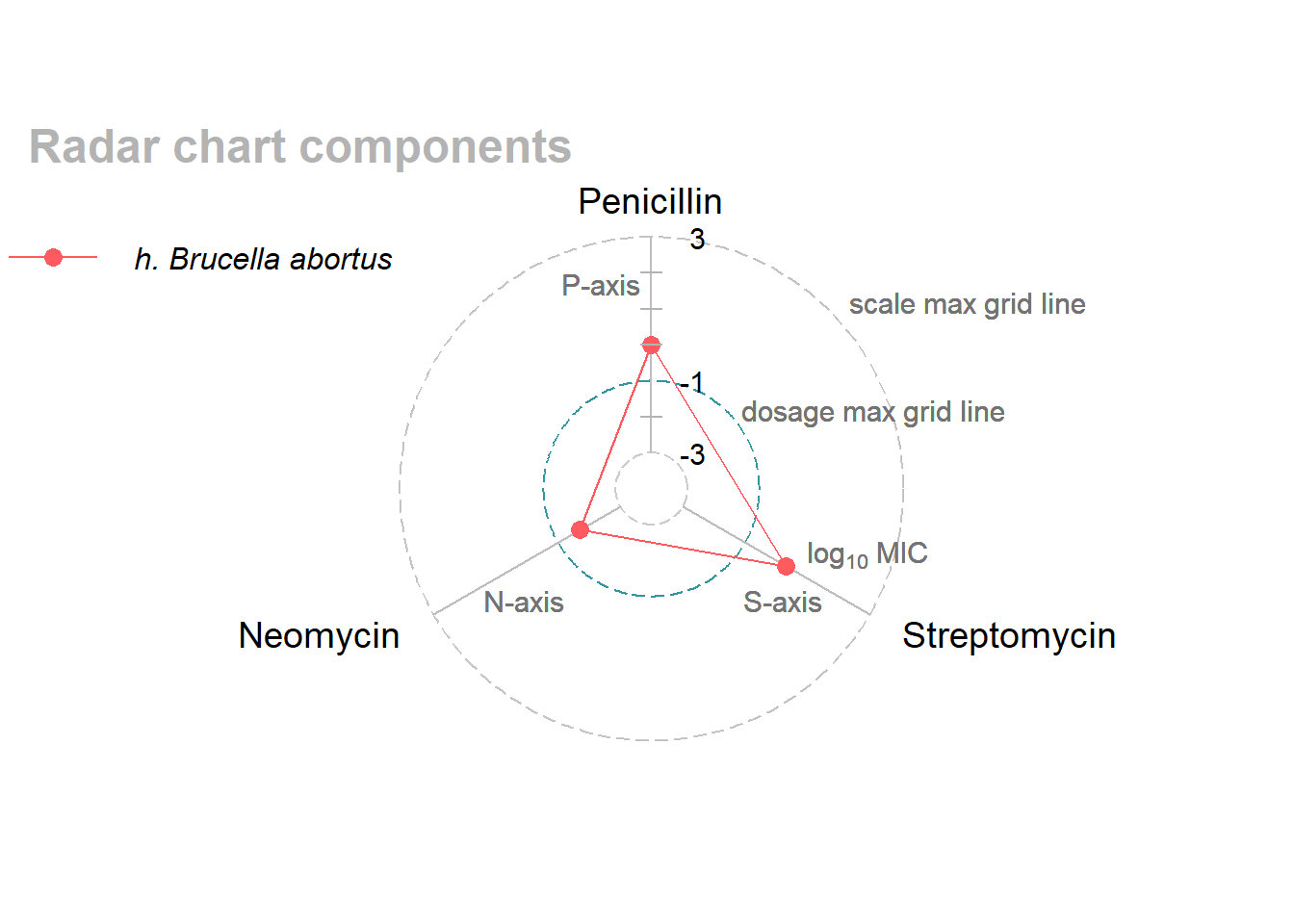
The axes of the chart encode the antibiotics: a P-axis (Penicillin), an S-axis (Streptomycin), and an N-axis (Neomycin). The three radial axes are rotated 120 degrees apart.
The axes have identical scales marked with log10MIC equal to –3, –1, and +3 and connected with circular grid lines. Reference tick marks are added to the P-axis in integer increments.
The log10 concentration values are encoded as data markers on the axes—in this example, 0.0 on the P-axis, +0.3 on the S-axis, and –1.7 on the N-axis.
Data markers inside the –1 grid line indicate clinically plausible MICs; points outside the line indicate resistance to the antibiotic. In this example, Brucella abortus is resistant to Penicillin and Streptomycin but not to Neomycin.
The thin helper lines between data markers create a polygon for that bacterium to help distinguish it from other bacteria when more than one are graphed in the same chart. The polygons, while useful visual aids, are not generally useful for drawing inferences about the data.
Creating the radar charts
I use the resistance variable to subset the data frame and construct one radar chart per group, yielding the five charts assembled in Figure 2. The legend keys verify that the charts retain the desired order of the bacteria, from (a) to (p) in order of increasing median MIC.
R code
data_group <- DT[resistance == "None"]
make_radar_chart(data_group, subtitle = "Resistant to None")
data_group <- DT[resistance == "P"]
make_radar_chart(data_group, subtitle = "Resistant to P")
data_group <- DT[resistance == "PS"]
make_radar_chart(data_group, subtitle = "Resistant to PS")
data_group <- DT[resistance == "PSN"]
make_radar_chart(data_group, subtitle = "Resistant to PSN")
data_group <- DT[resistance == "SN"]
make_radar_chart(data_group, subtitle = "Resistant to SN")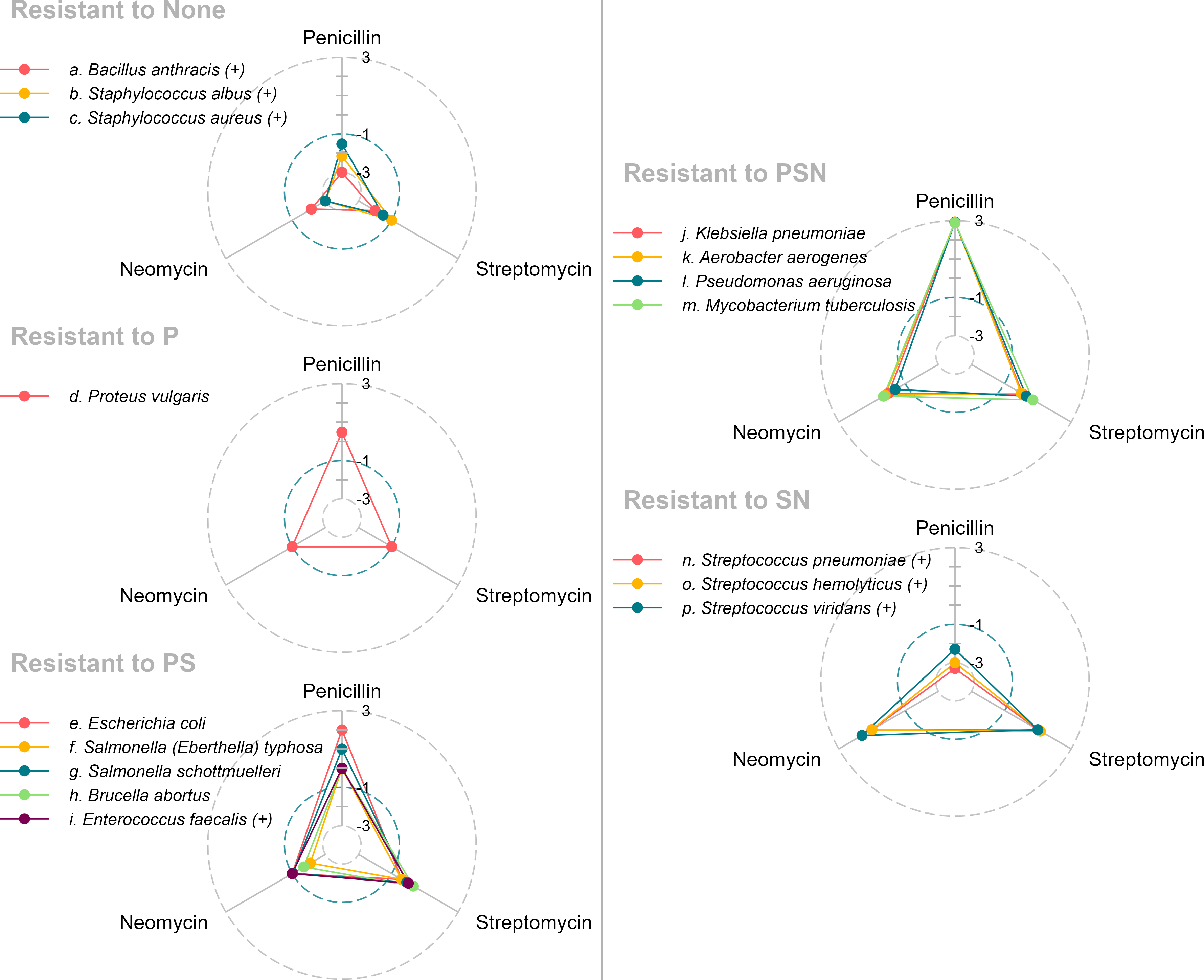
I assembled these images in a two-column format to make it possible to view all of them together. I made the font size as large as possible without overprinting important graphical elements. (The code for assembling the images is provided in an appendix.)
Faceted dot chart
Shaping the data
For compatibility with ggplot(), I transform the data from row records to block records. In block-record form, everything about a bacterium occupies a “block” of rows. For example, Bacillus anthracis occupies the first three rows instead of the first row alone as it did previously. The utility of this form is that both Antibiotic and Concentration are explicit variables with one value per observation (row).
R code
DT_facet <- melt(DT,
id.vars = c("Bacteria", "median_MIC", "resistance"),
variable.name = "Antibiotic",
variable.factor = FALSE,
value.name = "Concentration")
setcolorder(DT_facet, c("Bacteria", "Antibiotic", "Concentration", "median_MIC", "resistance"))
# order rows to illustrate block records
DT_facet[order(median_MIC, Bacteria)] Bacteria Antibiotic Concentration median_MIC
<char> <char> <num> <num>
1: a. Bacillus anthracis (+) Penicillin -3.00 -2.15
2: a. Bacillus anthracis (+) Streptomycin -2.00 -2.15
3: a. Bacillus anthracis (+) Neomycin -2.15 -2.15
4: b. Staphylococcus albus (+) Penicillin -2.15 -2.15
5: b. Staphylococcus albus (+) Streptomycin -1.00 -2.15
---
44: o. Streptococcus hemolyticus (+) Streptomycin 1.15 1.00
45: o. Streptococcus hemolyticus (+) Neomycin 1.00 1.00
46: p. Streptococcus viridans (+) Penicillin -2.30 1.00
47: p. Streptococcus viridans (+) Streptomycin 1.00 1.00
48: p. Streptococcus viridans (+) Neomycin 1.60 1.00
resistance
<char>
1: None
2: None
3: None
4: None
5: None
---
44: SN
45: SN
46: SN
47: SN
48: SNWe can add one more categorical variable (efficacy) to help visually distinguish between clinically plausible dosages (log10MIC ≤ –1) and bacterial resistance (log10MIC > -1) in the faceted dot chart. Table 3 lists the complete augmented set of variables.
R code
# efficacy variable used as legend key
DT_facet[, efficacy := fifelse(Concentration <= -1, "Effective", "Resistant")]| variable | structure |
|---|---|
| bacteria | categorical, nominal, 16 levels |
| antibiotic | categorical, nominal, 3 levels |
| min. inhibitory concentration (MIC) | quantitative (mg/dl) |
| Gram stain | categorical, 2 levels, dependent on bacteria |
| resistance profile | categorical, 5 levels, dependent on bacteria |
| efficacy | categorical, 2 levels, dependent on MIC |
Creating the faceted dot chart
Before plotting, I edit the data to order the rows and panels and add a resistance subtitle.
R code
# manually order the columns of the panel grid
DT_facet[, Antibiotic := lapply(.SD, factor, levels = c("Penicillin", "Streptomycin", "Neomycin")), .SDcols = "Antibiotic"]
# order the bacteria as a factor
DT_facet[, Bacteria := lapply(.SD, factor, levels = rev(sort(unique(Bacteria)))), .SDcols = "Bacteria"]
# add a subtitle for the resistance category
DT_facet[resistance == "None", resistance := "Resistant\nto\nNone"]The resulting chart has 15 facets in a 5 by 3 grid—five rows for the resistance variable and three columns for the antibiotic variable. Individual bacteria form an ordered vertical scale.
R code
# construct the faceted dot chart
ggplot(DT_facet, aes(x = Concentration, y = Bacteria, color = efficacy)) +
geom_point(size = 2) +
facet_grid(cols = vars(Antibiotic),
rows = vars(reorder(resistance, median_MIC)),
switch = "y",
scales = "free_y",
space = "free_y") +
# annotations
geom_vline(xintercept = -1, linetype = 2, linewidth = 0.5, color = "gray40") +
geom_text(data = DT_facet[resistance == "PSN"],
mapping = aes(x = -1, y = 1.5, label = c("max dose")),
vjust = -0.4, hjust = 0, angle = 90, color = "gray30", size = 3) +
# scales
scale_x_continuous(limits = c(-3.5, 3.5), breaks = seq(-3, 3, 2)) +
scale_color_manual(values = c("black", "gray")) +
scale_y_discrete(position = "right") +
labs(x = "MIC (log10 mg/dl)", y = "") +
# theme arguments
theme_minimal() +
theme(
# MIC scale
axis.text.x = element_text(size = 9),
# bacteria scale
axis.text.y = element_text(size = 9, hjust = 0, angle = 0, face = "italic"),
# antibiotic labels
strip.text.x = element_text(size = 10, hjust = 0),
# resistance labels
strip.text.y.left = element_text(size = 10, hjust = 1, angle = 0),
# panels
panel.border = element_rect(fill = NA, color = "gray90", linewidth = 0.7),
panel.spacing = unit(1, "mm"),
# legend
legend.position = "bottom",
legend.title = element_blank(),
legend.text = element_text(size = 12),
legend.key.size = unit(2, "mm")
)
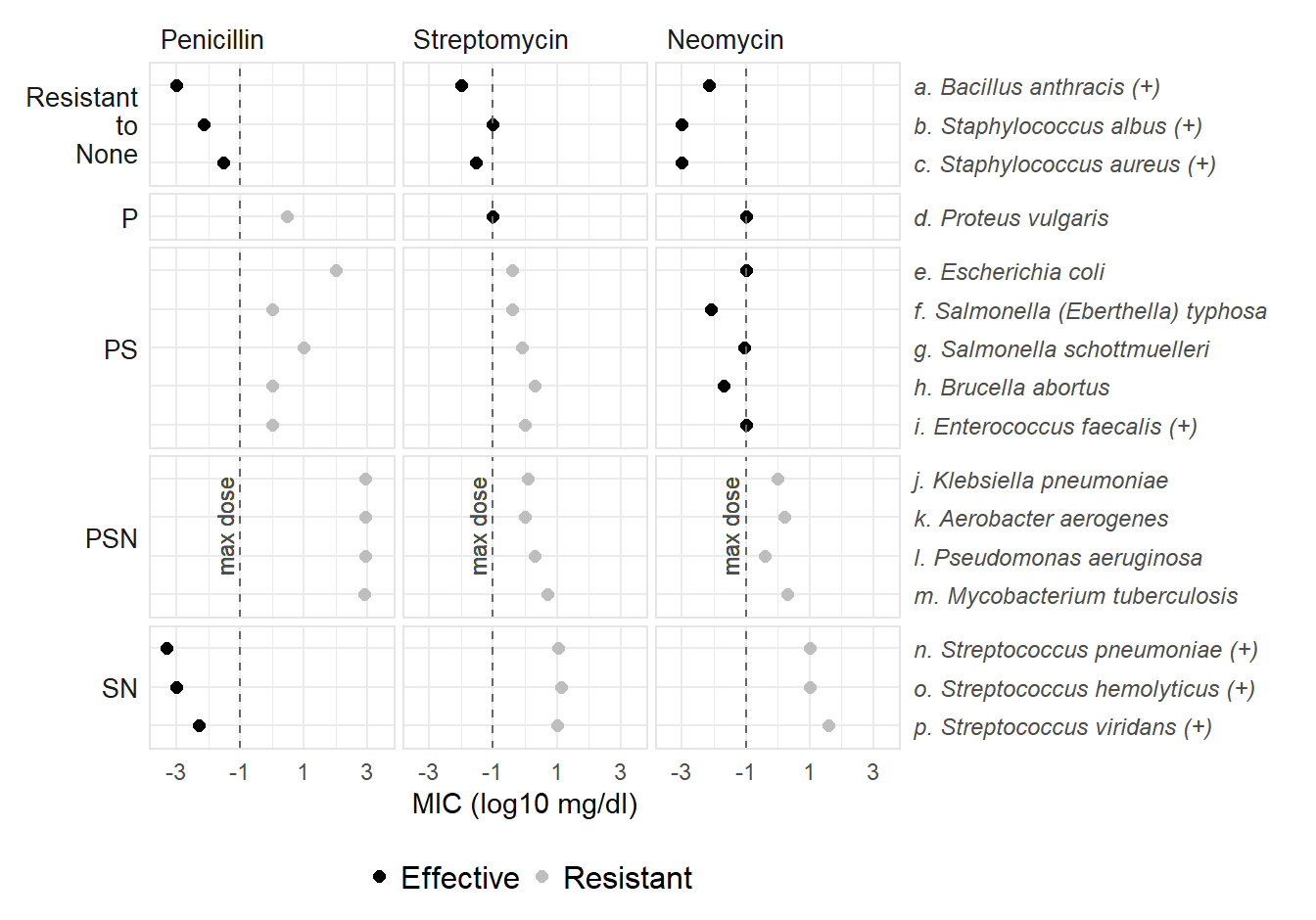
The log10MIC variable is encoded on identical horizontal scales. The maximum clinically plausible dosage is indicated with a vertical dashed line, separating interactions that are effective from those that are resistant.
For ggplot2 users, the interesting features of the code include:
facet_grid(switch = "y")withscale_y_discrete(position = "right")to place the bacteria labels on the right and the resistance category on the leftfacet_grid()argumentsscalesandspaceto create evenly spaced rows when, because of dependent categories, no facets are small multiples.
Discussion
Wainer poses five possible key questions that the data were gathered to answer (p. 30). Two of those questions arise naturally from the basic data structure—that MIC observations correspond to unique antibiotic-bacterium combinations. The first question focuses on the bacteria:
- How do the bacteria group vis-à-vis their reaction to the antibiotics?
As we have seen, grouping bacteria by their resistance profiles succeeds in revealing similarities. Both the radar chart and the faceted dot chart support this grouping visually: in the radar chart, by the similarity of polygons in an individual sub-plot; in the faceted chart, by the similarity of dot patterns in an individual facet.
The second question focuses on the antibiotics:
- How do the antibiotics group with respect to their efficacy in controlling the bacteria?
Consider first the efficacy of the drugs on one bacterium, e.g., item (g), Salmonella schottmeulleri. From the radar chart, we can infer that Neomycin is effective and that the other two drugs are resistant. However, the overprinting of data markers on the three axes makes it difficult to visually quantify the differences between the P-, S-, and N-value of MIC for this bacterium.
In contrast, in the faceted dot chart, data markers for a bacterium are located in a row with one row per bacterium and one panel per antibiotic. There is no overprinting. Looking along row (g), we again see that Neomycin is effective and the others are resistant but we can also visually estimate the MIC values using the horizontal scale: Neomycin log10MIC ≈ –1, Streptomycin ≈ 0, and Penicillin ≈ 1.
The faceted chart, compared to the radar chart, makes such differences easier to quantify. Adding more circular grid lines to the radar chart might improve our ability to estimate its MIC values, but the radar chart has an intrinsic potential for data markers (and the polygons) overprinting one another.
Second, let’s consider differential efficacy of the drugs across groupings. For example, for how many of the resistance-groupings is penicillin effective? Using the radar charts, we examine the P-axis of all 5 charts and conclude that Penicillin is effective in two of the groupings. (The names of the groupings tell us this as well, but here I want to focus on the effectiveness of the visualization.)
In the faceted chart, the five panels in the Penicillin column yield the same conclusion at a glance.
Wainer’s other three questions are:
- What bacterium does this antibiotic kill?
- What antibiotic kills this bacterium?
- Does the “Gram staining” variable help us make decisions regarding which antibiotic to use?
All three questions can be answered by both charts, but generally more quickly and clearly using the faceted dot chart. I leave the details of that comparison to the reader.
In general, the advantages of the faceted dot chart include:
- Horizontal grid lines suffice to distinguish one bacterium from another.
- Greater visual access to patterns of data in different combinations.
- Relatively compact without sacrificing readability.
- Data markers do not overprint one another.
- Conventional horizontal scales.
Conclusion
Using Will Burtin’s 1951 data on the efficacy of three antibiotics on 16 bacteria (with updated bacteria taxonomy), I compared the effectiveness of two types of charts by considering the ease and accuracy of answering key domain-specific questions.
By using the same data organized in the same way, both charts are designed to convey the same message. Thus any differences in perceived effectiveness should be due to differences in chart structure, that is, characteristics of the chart intrinsic to its type.
For the data at hand, a faceted dot chart communicates more effectively than a radar chart. Intrinsic differences between the two chart types suggest that in general appropriately configured dot charts are more effective than radar charts.
Additional software credits
Image processing with magick
The following code chunk is provided for readers interested in the image processing I used to assemble the five radar charts into one figure. As usual in R, there are several ways to approach this task; here I use “magick,” an R package for advanced graphics and image processing.
R code
# image processing using the magick package
library(magick)
# custom functions
trim_radar <- function(data_group, subtitle, img_path, name_png) {
p <- make_radar_chart(data_group, subtitle)
ggsave_radar(p, img_path, name_png)
img <- image_read(paste0(img_path, name_png))
img <- image_trim(img)
}
ggsave_radar <- function(p, img_path, name_png) {
ggsave(
plot = p,
path = img_path,
filename = name_png,
width = 6.8,
height = 5,
units = "in"
)
}
# local path to figures
img_path <- "posts/2022-08-15-radar-charts/figures/"
# create individual radar charts
img1 <- trim_radar(data_group = DT[resistance == "None"],
subtitle = "Resistant to None",
img_path = img_path,
name_png = "none.png")
img2 <- trim_radar(data_group = DT[resistance == "P"],
subtitle = "Resistant to P",
img_path = img_path,
name_png = "p.png")
img3 <- trim_radar(data_group = DT[resistance == "PS"],
subtitle = "Resistant to PS",
img_path = img_path,
name_png = "ps.png")
img4 <- trim_radar(data_group = DT[resistance == "PSN"],
subtitle = "Resistant to PSN",
img_path = img_path,
name_png = "psn.png")
img5 <- trim_radar(data_group = DT[resistance == "SN"],
subtitle = "Resistant to SN",
img_path = img_path,
name_png = "sn.png")
# white box same width as figure to vertically offset second column
w <- image_info(img1)[["width"]]
h <- image_info(img1)[["height"]]
box <- image_blank(width = w, height = h * 0.5, color = "white")
# thin vertical separation strip
white_strip <- image_blank(width = 30, height = h, color = "white")
gray_strip <- image_blank(width = 5, height = h, color = "gray70")
# assemble composite figure
img1 <- image_append(c(img1, white_strip, gray_strip, white_strip), stack = FALSE)
img2 <- image_append(c(img2, white_strip, gray_strip, white_strip), stack = FALSE)
img3 <- image_append(c(img3, white_strip, gray_strip, white_strip), stack = FALSE)
col_1 <- image_append(c(img1, img2, img3), stack = TRUE)
col_2 <- image_append(c(box, img4, img5), stack = TRUE)
img <- image_append(c(col_1, col_2), stack = FALSE)
# write final image to file
image_write(img, path = paste0(img_path, "five_radar.png"))References
Few, S. (2005). Keep radar graphs below the radar—far below. Newsletter. https://www.perceptualedge.com/articles/dmreview/radar_graphs.pdf
Odds, G. (2011). A critique of radar charts. Blog post. https://blog.scottlogic.com/2011/09/23/a-critique-of-radar-charts.html
Wainer, H. (2014). Medical Illuminations. Oxford University Press.